|
|
|

Modes n' Scales
Modal
Theory
The
term “mode” refers to a set of notes that can be derived from a specific
scale. For example, the C major scale is spelled C D E F G A B; this is also
known as the C Ionian mode. If you were to take this same set of notes and start
from the second scale degree, D, and continue up to D one octave higher, the
resultant “scale” is known as the D Dorian mode (D E F G A B C) (see FIGURE
1). As you can see and hear, both modes (C Ionian and D Dorian) are composed of
the same seven notes, the only difference being the way they’re oriented.

This same modal relativity concept can be applied to each degree of the C major
scale: if we begin on the third scale degree, E, and continue through the same
note series to E one octave higher, we’d be playing the E Phrygian mode (E F G
A B C). The remaining modes that are built from the C major scale are F Lydian
(F G A B C D E), G Mixolydian (G A B C D E F), A Aeolian (A B C D E F G) and B
Locrian (B C D E F G A). These seven modes—Ionian, Dorian, Phrygian, Lydian,
Mixolydian, Aeolian and Locrian—are all simply different orientations of the
“parent” major scale, each beginning on a different scale degree, and are
known collectively as the “fundamental modes.”
I
used this particular scale to illustrate the theory of the fundamental modes
because, unlike the other major scales, it contains no sharps or flats and is
easier to “think in.” Realize, however, that this same principle of modal
relativity applies to every key, not just C. For example, the G major scale (G A
B C D E F#) spawns seven modes, one for each note of the scale.

Though
thinking of a mode as being the same as some other major scale is a very useful
learning device, it is only when one fully understands and internalizes the
sound of each mode’s intervallic structure that one will master the modal
concept. One day, back when was in my first year of music college, I was taking
a piano lesson when my teacher and I came to a particular section of
improvisation. I said, “This is in the A Dorian mode.” My teacher said,
“Well, it’s really the same as playing in G major,” but I disagreed. I
said that if I’m playing in A Dorian, I’ll emphasize the notes differently
than if I were thinking G major.
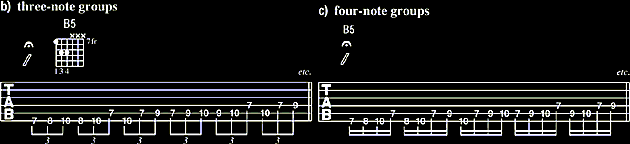
As
I began to study the seven fundamental modes, I became fascinated with the
differences in their intervallic structures and the inherent chord forms that
can be constructed out of them. I also liked to compare them by playing them off
of the same root note (as parallel modes, as opposed to relative modes). I
discovered that certain modes were nearly identical in form, except for a single
interval. An example of this would be the E Phrygian (E F G A B C) and E Aeolian
(E F# G A B C D) modes, the former being the third mode of the C major scale and
the latter being the sixth mode of the G major scale. Comparing modes this
way—back to back, in the same key—helped me understand the differences in
their structure and sound.

The
whole point of studying theory and harmony should be to discover more ways to
better express one’s own musical vision.
As
illustrated in FIGURES 2a and 2b, this mode is theoretically formed by taking
the G major scale and using the third, B, as the root note. FIGURE 3a
illustrates the B Phrygian mode in the seventh position. Memorize this fingering
pattern by playing it up and down repeatedly. The exercises depicted in FIGURES
3b-3e are intended to get the unique sound of the B Phrygian mode into your
mind.
==============================================================
Mode
Swings more on modal theory
In
terms of modal study, the modes only have meaning when they’re addressed and
understood as entities unto themselves, not as permutations of any “parent”
scale. Whatever the root note of a particular mode may be—for example, B in
the B Phrygian mode—that root note must be made clear to the listener in order
for the unique harmonic texture of a given mode to be experienced by the
listener. It is only when a mode is heard against a particular root note or
tonal center that its quality can be understood. Its position or fingering on
the fret board is irrelevant to the listener.

For
example, FIGURE 1a illustrates a G major scale with the B Phrygian mode
extracted from it. You’ll notice that B Phrygian is built from the third note
of the G major scale, so Phrygian is logically known as the third mode of the
major scale. If we play a C note within the context of B Phrygian, the function
of this note is entirely different than if it were played within the context of
G major. When C is played over G, as illustrated in FIGURE 1b, it’s heard as
the fourth, as in a Gsus4 chord (G C D).
Playing
C over B Phrygian is an entirely different matter. When C is played over B, it
functions as both the minor, or “flatted,” second or ninth (“b2” or
“b9”). The sound of a C note played over a B root is very dissonant and is
totally unlike the suspended fourth sound of C played over a G tonal center. To
illustrate this point, FIGURE 1c shows the notes B and C played as flatted
seconds/ninths and also illustrates how C functions as the “b9” over a B
root note in two commonly used chords.

Reference: Engine of Creation by Joe Satriani